Das Experiment
Das Münzwurfexperiment wird von Victor Haghani und Richard Dewey in deren Paper „Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin“ beschrieben. [1] Haghani ist in der Finanzindustrie bekannt: Er zählte einst zu den Gründungspartnern des gescheiterten Hedgefonds LTCM.
Vor Spielbeginn bekamen die insgesamt 61 Teilnehmer den klaren Hinweis, dass die simulierte Münze eine 60-prozentige Wahrscheinlichkeit für Kopf und eine 40-prozentige Wahrscheinlichkeit für Zahl hat. Das Startkapital betrug jeweils 25 US-Dollar. Es wurde erklärt, dass man das Guthaben vorbehaltlich eines Maximalbetrags am Ende des Spiels ausgezahlt bekommt. Das Maximum lag bei 250 US-Dollar und wurde den Spielern erst konkret mitgeteilt, wenn sie diesen Betrag erreichen, um die vorherige Erwartungshaltung nicht zu verzerren.
Die Ergebnisse
Die Teilnehmer des Experiments waren größtenteils Wirtschaftsstudenten und junge Fachkräfte aus Finanzunternehmen. Man konnte also annehmen, dass sie gut darauf vorbereitet sein sollten, ein einfaches Spiel mit festem positivem Erwartungswert zu spielen. Doch die Ergebnisse hielten eine faustdicke Überraschung bereit.
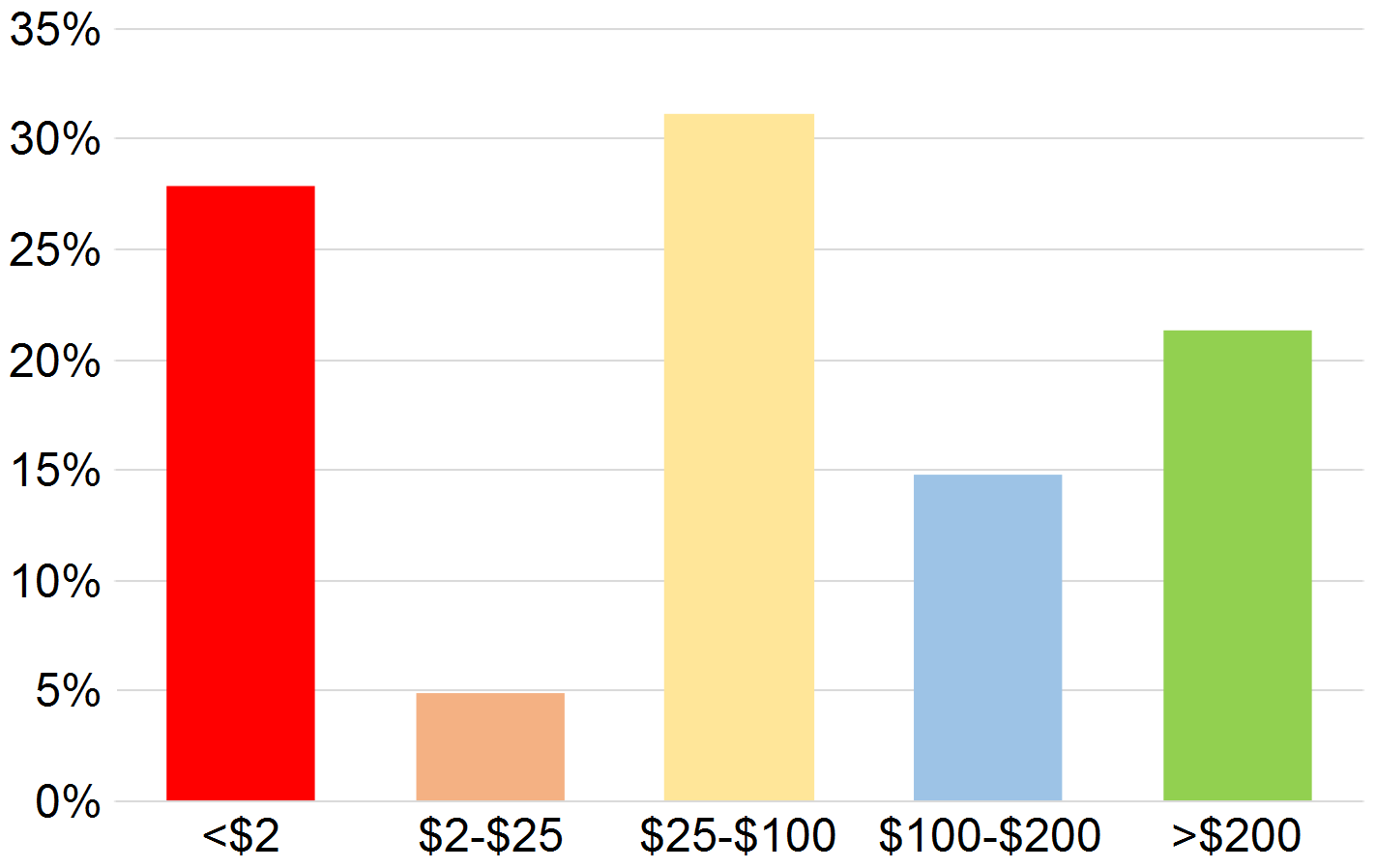
Die Grafik zeigt die Verteilung des Endvermögens nach 30 Minuten Spielzeit. Grob lassen sich drei Kategorien einteilen: Zocker (links in rot), Konservative (Mitte in gelb) und Strategen mit optimalem Setzverhalten (rechts in grün).
Quelle: Haghani, V. / Dewey, R. (2016), Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin, S. 4
Die Teilnehmer platzierten suboptimale Wetten in allen Formen und Größen: zu hohe und zu niedrige Einsätze, erratisches Setzverhalten und irrationales Setzen auf Zahl statt Kopf. Auf diese Weise verspielten die meisten ihre Chance, nach der halben Stunde Spielzeit mit 250 Dollar nach Hause zu gehen. Tatsächlich erreichten nur 21 Prozent der Teilnehmer dieses Maximum. Noch erstaunlicher war aber die Tatsache, dass 28 Prozent der Teilnehmer nahezu oder komplett Pleite gingen (Restwert unter 2 Dollar).












