Man könnte glauben, dass Zahlen niemals lügen, wenn die entsprechenden Berechnungen keine Fehler beinhalten. Und das ist objektiv betrachtet auch korrekt. Doch Statistiken allein können uns dennoch täuschen, wenn sie ein unvollständiges Bild von der Realität zeigen – oder wenn wir sie falsch interpretieren.
Als Menschen sind wir zudem nicht besonders gut darin, mit Zahlen zu arbeiten, und können visuelle Darstellungen viel schneller und besser einordnen. Der kurze Blick auf den Chartverlauf einer Aktie verdeutlicht das eindrucksvoll, verglichen mit der Alternative, die nackten Kursdaten langwierig in einer Excel-Tabelle auf ihren Trend hin zu analysieren. Die Zahlen mögen exakter sein, aber die grobe Einordnung grafischer Darstellungen erfolgt dafür in Sekundenschnelle.
Dass aber selbst Statistiken nicht immer so exakt sind, wie sie vielen erscheinen, zeigte Francis Anscombe schon in seiner im Jahr 1973 erschienen Studie „Graphs in Statistical Analysis“. Darin sind verschiedene Beispiele aufgeführt, die verdeutlichen, warum neben reinen Statistiken unbedingt auch grafische Darstellungen in die Analyse einzubeziehen sind.
Anscombe's Quartett
Ein zentrales Problem ist, dass Statistiken auf Annahmen beruhen. Und wenn diese Annahmen falsch sind, dann haben auch die darauf basierenden Berechnungen keinen Wert – oder schlimmer noch, sie führen uns in die Irre. Die folgende Grafik zeigt passend dazu das Beispiel aus der Studie von Anscombe.
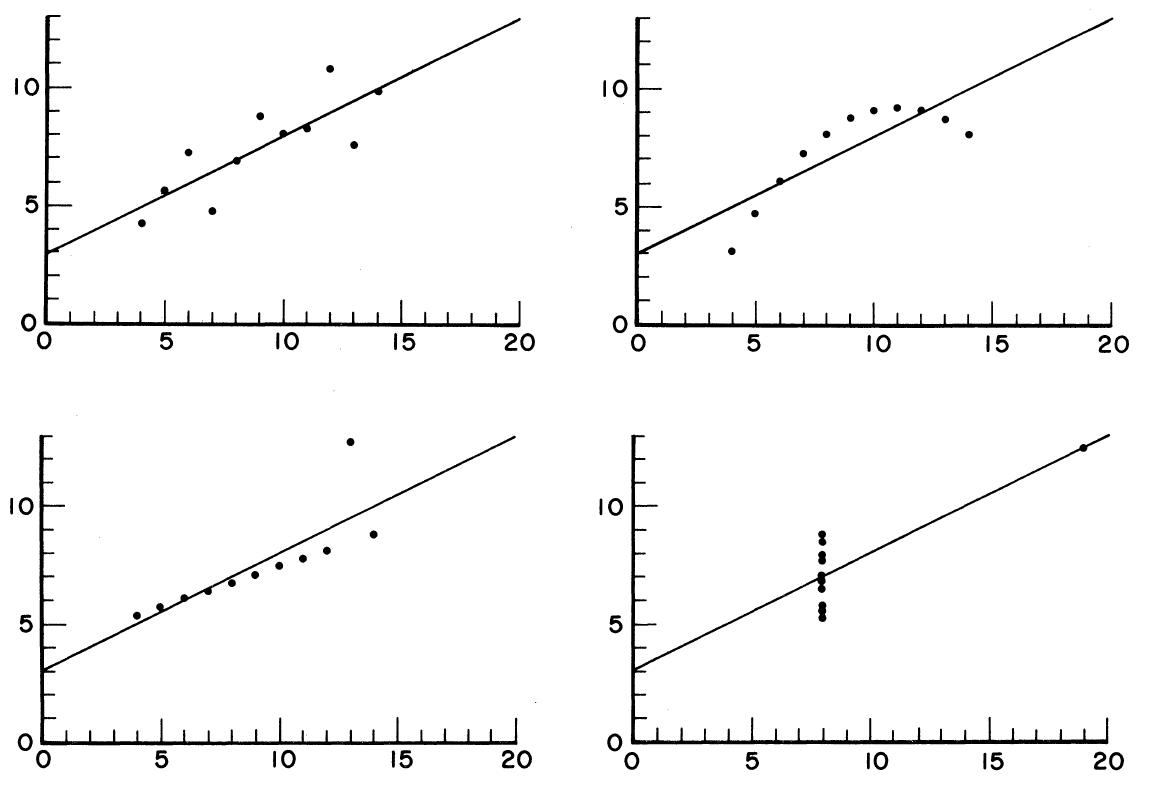
Die einzelnen Diagramme zeigen verschiedene Verteilungen von Datenpunkten (linear, nichtlinear, Ausreißer). Vor einer statistischen Analyse sollte visuell überprüft werden, ob die getroffenen Annahmen überhaupt stimmig sind.
Quelle: Anscombe, F. J. (1973), Graphs in Statistical Analysis, American Statistician, Vol. 27, Nr. 1, S. 19-20
Offensichtlich sind die vier Datensätze sehr unterschiedlich. Umso erstaunlicher ist aber folgende Tatsache: Jagt man die Rohdaten durch ein Statistik-Programm, ergeben sich identische Ergebnisse für den Mittelwert, die Korrelation und die Regressionsgleichung.
Es wäre verheerend, die Interpretation nur auf Grundlage der Statistiken durchzuführen. Erst der Blick auf die grafische Darstellung offenbart, dass für die einzelnen Datensätze völlig unterschiedliche Interpretationen notwendig sind. Das Beispiel zeigt, wie bestimmte Anordnungen von Datenpunkten irreführende Statistiken ergeben und einzelne Ausreißer das Ergebnis extrem beeinflussen können.
Dieses Prinzip lässt sich auf Börsenkurse übertragen. Viele Anleger arbeiten mit Charts, um einen schnellen Überblick zum Kursverlauf zu erhalten und gegebenenfalls weitere Analysen durchzuführen. Die wenigsten verlassen sich allein auf Kennzahlen, egal ob fundamentaler oder technischer Natur, oder bereiten diese zumindest ebenfalls visuell auf. Und das aus gutem Grund: Die Kombination von Kennzahlen und Charts hat sich in der Praxis als „Common Sense“ im Sinne der Entscheidungsfindung auf Basis des gesunden Menschenverstands bewährt.
Monty Hall
Ein anderes Beispiel, in dem sich die meisten Menschen täuschen, ist das Monty-Hall-Problem. Dieses wurde erstmals im Jahr 1975 in einer Kolumne beschrieben, aber hat bis heute nichts von seiner Faszination verloren. Denn hier liegen selbst Experten, die sich mit Wahrscheinlichkeiten bestens auskennen, regelmäßig falsch. Schon damals meldeten sich im Anschluss an die Veröffentlichung der Lösung unzählige Leute und meinten, dass die präsentierte Lösung falsch sei, darunter auch promovierte Wissenschaftler. Doch es war alles korrekt.
Die nachfolgende Grafik zeigt die Ausgangslage. Angenommen, es gibt ein Gewinnspiel mit drei Türen. Hinter einer Tür verbirgt sich der Gewinn (ein Auto), hinter den beiden anderen Nieten (Ziegen). Wir wählen nun zufällig eine Tür aus, beispielsweise Tür 1. Der Moderator, der weiß, was hinter den Türen ist, öffnet nun eine andere Tür, nämlich Tür Nummer 2. Dahinter verbirgt sich eine Niete. Dann fragt er, ob wir nun unseren Tipp für den Gewinn von Tür 1 zu Tür 3 wechseln möchten oder nicht.
Die entscheidende Frage ist nun: Wäre der Wechsel ein Vorteil?
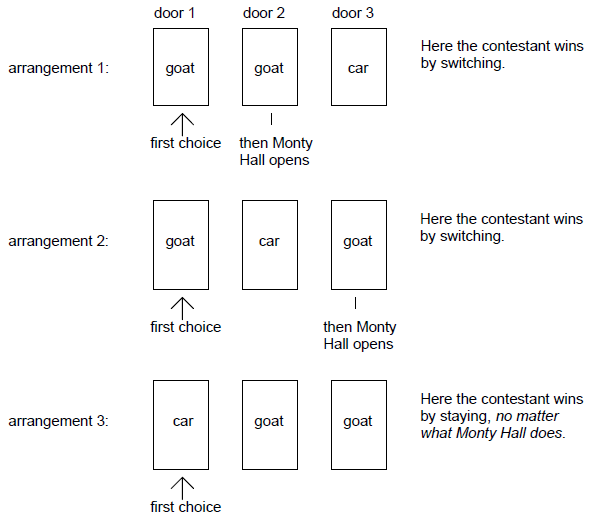
In zwei von drei Fällen bekommt man den Gewinn, wenn die gewählte Tür gewechselt wird.
Quelle: Krauss, S. / Wang, X. T. (2003), The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser, Journal of Experimental Psychology General, Vol. 132, Nr. 1
Die Antwort: Ja, man sollte zu Tür 3 wechseln. Dann ist die Wahrscheinlichkeit für den Gewinn 2/3.
Auf den ersten Blick ist es schwer, das nachzuvollziehen. Intuitiv sollten sowohl Tür 1 als auch Tür 3 eine jeweils 50-prozentige Wahrscheinlichkeit für den Gewinn haben, da Tür 2 offengelegt wurde. Aber dem ist nicht so.
Die Erklärung: Wir hatten uns auf Tür 1 festgelegt. Der Moderator kann diese also nicht öffnen. Ebenso kann er keine Tür öffnen, hinter der sich der Gewinn verbirgt, da das Spiel dann vorbei wäre. Diese Restriktionen machen Tür 3 gegenüber den zuvor gleichverteilten Wahrscheinlichkeiten nun attraktiver:
Ist der Gewinn hinter Tür 3, kann der Moderator nur Tür 2 öffnen und das Wechseln lohnt sich.
Ist der Gewinn hinter Tür 2, kann er nur Tür 3 öffnen und das Wechseln lohnt sich (in diesem Fall Wechsel zu Tür 2).
Der einzige der 3 Fälle, in dem sich das Wechseln nicht lohnt, ist, wenn der Gewinn hinter der bereits gewählten Tür 1 ist.
Damit gewinnt man in zwei von drei Fällen durch das Wechseln der Tür, also mit einer Wahrscheinlichkeit von 2/3. Die anfängliche Intuition hat hier also tatsächlich getäuscht.
Zinseszinseffekt
Der klassische Effekt, bei dem wir uns als Menschen intuitiv täuschen, ist das „Achte Weltwunder“ nach Albert Einstein, der Zinseszinseffekt. Aber kann es wirklich so schwer sein, zu verstehen, wie er sich auswirkt? Schließlich lernt man dessen Berechnung schon früh in der Schule.
Das Problem: Dem linear denkenden menschlichen Gehirn ist es von Natur aus praktisch unmöglich, exponentielle Zusammenhänge richtig zu erfassen. Wissen allein nützt also nicht viel, wenn man die immensen Auswirkungen nicht selbst erlebt und verinnerlicht hat.
Auch dazu ein Beispiel: Angenommen, wir haben ein Blatt Papier mit einem Durchmesser von 0,1 Millimeter, das beliebig oft gefaltet werden kann. Wie oft müsste man dieses Blatt ungefähr falten, damit der resultierende Papierstapel rechnerisch bis zum Mond (mittlere Entfernung rund 384.000 Kilometer) reicht?
Die verblüffende Antwort: 42 Mal. Und damit wären wir sogar schon „hinter dem Mond“. Wer es nicht glaubt, kann gern nachrechnen: 0,1 Millimeter x 2^42 ergibt rund 440.000 Kilometer.
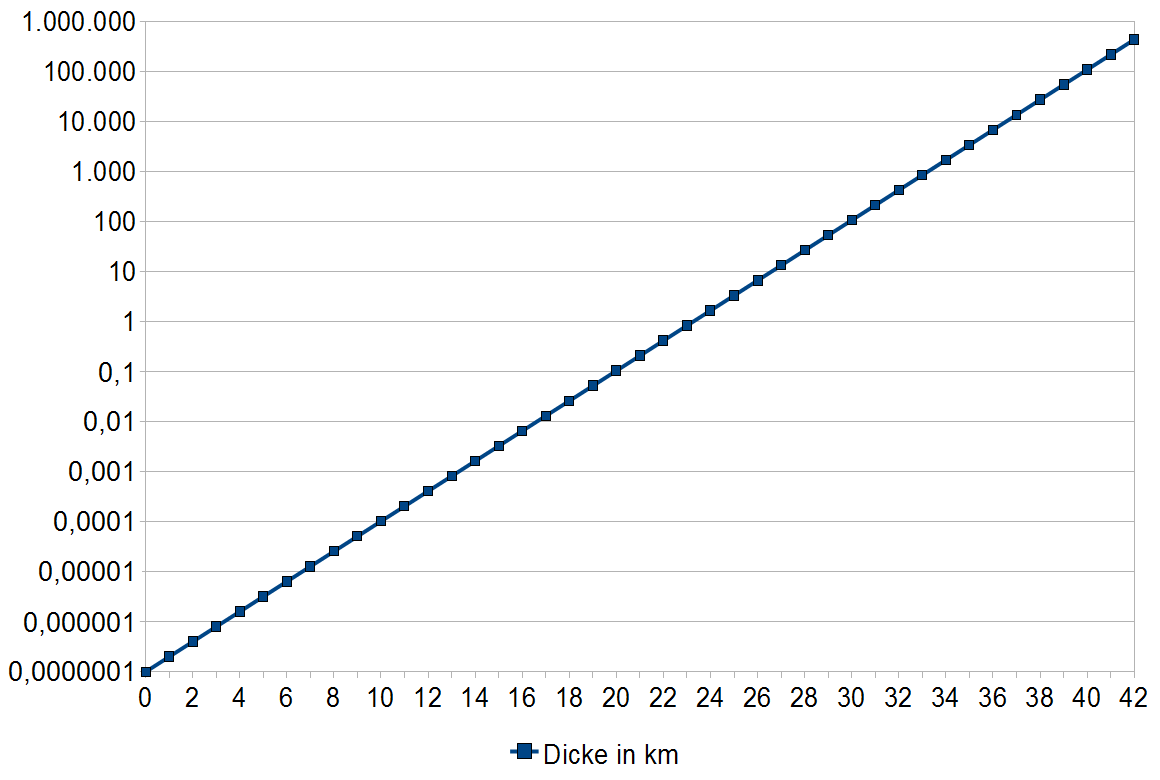
Ein 0,1 Millimeter dünnes Blatt, 42 Mal gefaltet, ergibt rechnerisch einen Papierstapel, der bis über den Mond hinaus reicht.
Quelle: eigene Berechnungen des Autors
Ähnlich verhält es sich bei einem Schachbrett, auf dessen erstem Feld ein Reiskorn liegt. Dann wird die Anzahl auf jedem Feld verdoppelt. Für das letzte Feld mit der Nummer 64 ist das Ergebnis ebenfalls nur theoretischer Natur, denn die Menge der weltweit überhaupt verfügbaren Reiskörner ist dort schon lange überschritten.
Fazit
Es lohnt sich immer, Statistiken und grafische Darstellungen gegeneinander abzugleichen und in Kombination zu interpretieren, um keinem Trugschluss aufzusitzen. Doch auch der gesunde Menschenverstand kann uns täuschen, insbesondere wenn es um exponentielle Zusammenhänge geht. In diesem Fall lohnt sich das Nachrechnen, statt der Intuition zu folgen.












